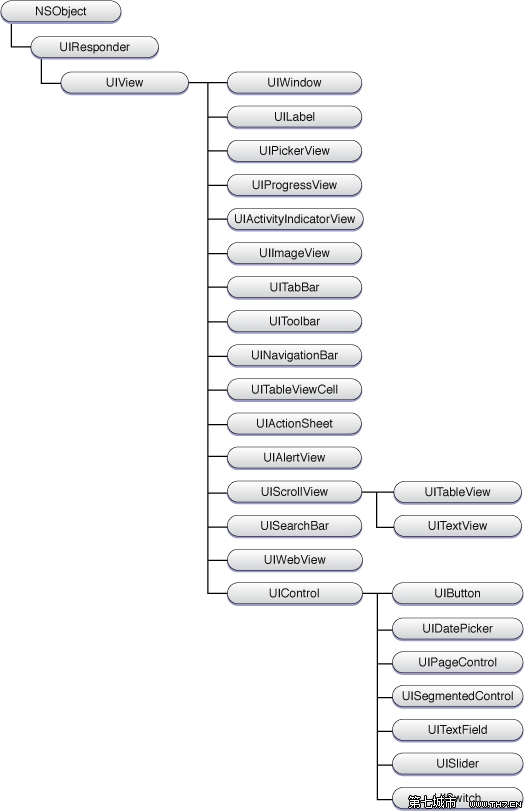
初识A*算法
Sunway
目 录
1 何谓启发式搜索算法
2 初识A*算法
写这篇文章的初衷是应一个网友的要求,当然我也发现现在有关人工智能的中文站点实在太少,我在这里抛砖引玉,希望大家都来热心的参与。还是说正题,我 先拿A*算法开刀,是因为A*在游戏中有它很典型的用法,是人工智能在游戏中的代表。A*算法在人工智能中是一种典型的启发式搜索算法,为了说清楚A*算 法,我看还是先说说何谓启发式算法。
1、何谓启发式搜索算法
在说它之前先提提状态空间搜索。状态空间搜索,如果按专业点的说法就是将问题求解过程表现为从初始状态到目标状态寻找这个路径的过程。通俗点说,就是 在解一个问题时,找到一条解题的过程可以从求解的开始到问题的结果(好象并不通俗哦)。由于求解问题的过程中分枝有很多,主要是求解过程中求解条件的不确 定性,不完备性造成的,使得求解的路径很多这就构成了一个图,我们说这个图就是状态空间。问题的求解实际上就是在这个图中找到一条路径可以从开始到结果。 这个寻找的过程就是状态空间搜索。
常用的状态空间搜索有深度优先和广度优先。广度优先是从初始状态一层一层向下找,直到找到目标为止。深度优先是按照一定的顺序前查找完一个分支,再查找另一个分支,以至找到目标为止。这两种算法在数据结构书中都有描述,可以参看这些书得到更详细的解释。
前面说的广度和深度优先搜索有一个很大的缺陷就是他们都是在一个给定的状态空间中穷举。这在状态空间不大的情况下是很合适的算法,可是当状态空间十分大,且不预测的情况下就不可取了。他的效率实在太低,甚至不可完成。在这里就要用到启发式搜索了。
启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径,提 到了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。我们先看看估价是如何表示的。
启发中的估价是用估价函数表示的,如:
| f(n) = g(n) + h(n) |
其中f(n) 是节点n的估价函数,g(n)实在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。在这里主要是h(n)体现了搜 索的启发信息,因为g(n)是已知的。如果说详细点,g(n)代表了搜索的广度的优先趋势。但是当h(n) >> g(n)时,可以省略g(n),而提高效率。这些就深了,不懂也不影响啦!我们继续看看何谓A*算法。
2、初识A*算法
启发式搜索其实有很多的算法,比如:局部择优搜索法、最好优先搜索法等等。当然A*也是。这些算法都使用了启发函数,但在具体的选取最佳搜索节点时的 策略不同。象局部择优搜索法,就是在搜索的过程中选取“最佳节点”后舍弃其他的兄弟节点,父亲节点,而一直得搜索下去。这种搜索的结果很明显,由于舍弃了 其他的节点,可能也把最好的节点都舍弃了,因为求解的最佳节点只是在该阶段的最佳并不一定是全局的最佳。最好优先就聪明多了,他在搜索时,便没有舍弃节点 (除非该节点是死节点),在每一步的估价中都把当前的节点和以前的节点的估价值比较得到一个“最佳的节点”。这样可以有效的防止“最佳节点”的丢失。那么 A*算法又是一种什么样的算法呢?其实A*算法也是一种最好优先的算法。只不过要加上一些约束条件罢了。由于在一些问题求解时,我们希望能够求解出状态空 间搜索的最短路径,也就是用最快的方法求解问题,A*就是干这种事情的!我们先下个定义,如果一个估价函数可以找出最短的路径,我们称之为可采纳性。A* 算法是一个可采纳的最好优先算法。A*算法的估价函数可表示为:
| f'(n) = g'(n) + h'(n) |
这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值,h'(n)是n到目标的最断路经的启发值。由于这个f'(n)其实是无法预先知道 的,所以我们用前面的估价函数f(n)做近似。g(n)代替g'(n),但 g(n)>=g'(n)才可(大多数情况下都是满足的,可以不用考虑),h(n)代替h'(n),但h(n)<=h'(n)才可(这一点特别 的重要)。可以证明应用这样的估价函数是可以找到最短路径的,也就是可采纳的。我们说应用这种估价函数的最好优先算法就是A*算法。哈。你懂了吗?肯定没 懂。接着看。
举一个例子,其实广度优先算法就是A*算法的特例。其中g(n)是节点所在的层数,h(n)=0,这种h(n)肯定小于h'(n),所以由前述可知广度优先算法是一种可采纳的。实际也是。当然它是一种最臭的A*算法。
再说一个问题,就是有关h(n)启发函数的信息性。h(n)的信息性通俗点说其实就是在估计一个节点的值时的约束条件,如果信息越多或约束条件越多则排除 的节点就越多,估价函数越好或说这个算法越好。这就是为什么广度优先算法的那么臭的原因了,谁叫它的h(n)=0,一点启发信息都没有。但在游戏开发中由 于实时性的问题,h(n)的信息越多,它的计算量就越大,耗费的时间就越多。就应该适当的减小h(n)的信息,即减小约束条件。但算法的准确性就差了,这 里就有一个平衡的问题。可难了,这就看你的了!
好了我的话也说得差不多了,我想你肯定是一头的雾水了,其实这是写给懂A*算法的同志看的。哈哈。你还是找一本人工智能的书仔细看看吧!我这几百字是不足以将A*算法讲清楚的。只是起到抛砖引玉的作用希望大家热情参与吗。